Z dat jsou užita pouze pozorování překračující stanovenou mez, například 95 % kvantil.
Úloha
Nahrajte do prostředí data z klementiské řady měření
Metodou blokových maxim stanovte maxima
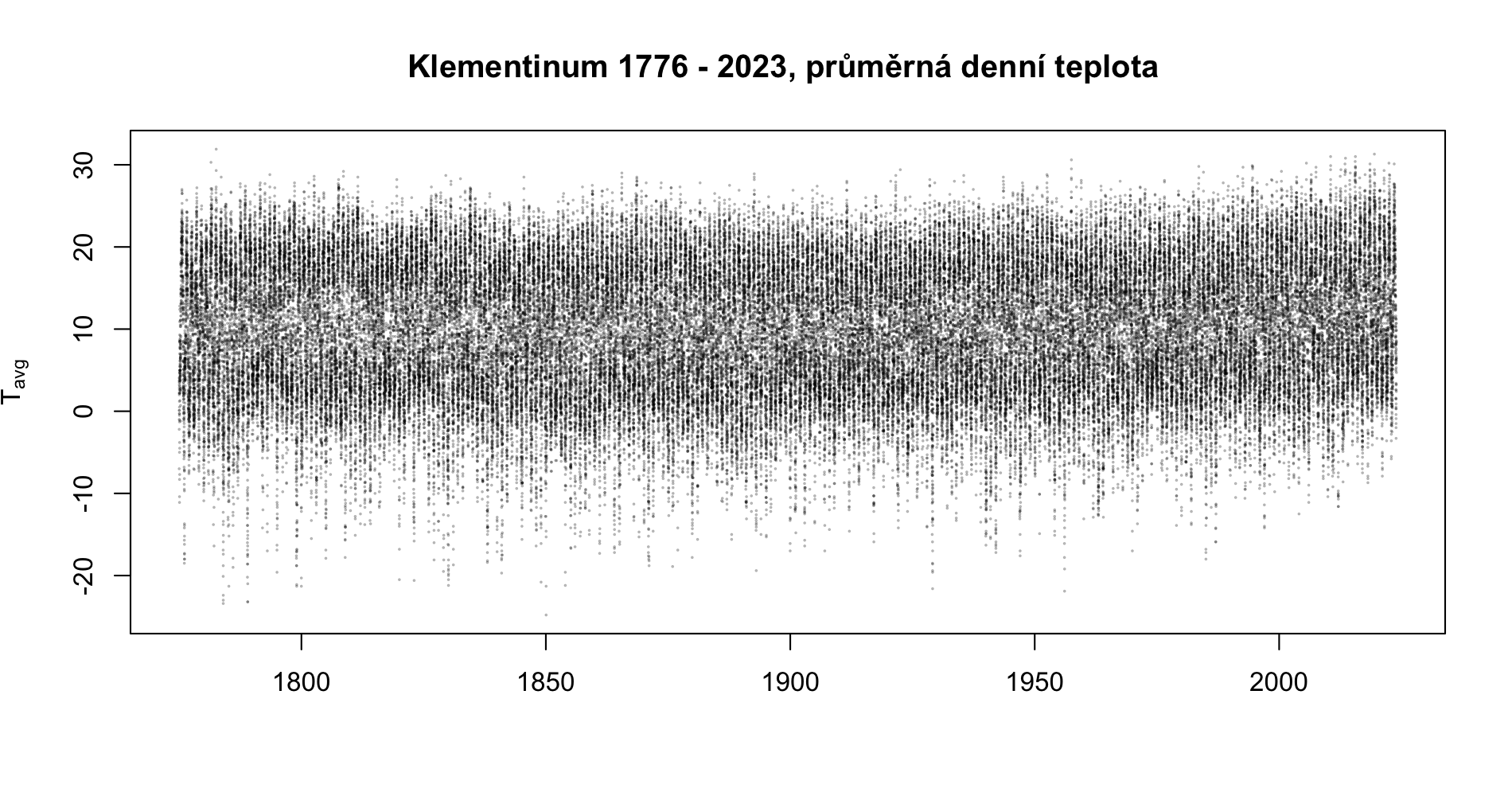
Kód
klementinum_short <- klementinum |> dplyr::filter(yr %in%2000:2020) window <-2000:2020i <-seq(from =as.Date("2000-01-01"), to =as.Date("2020-12-31"), by ="1 year")j <-ifelse(as.numeric(i) %%2==0, "black", "#00000090")plot(main ="Klementinum 1776 - 2023", sub ="Identifikace extrémů s pomocí blokových maxim", x = klementinum_short$date,y = klementinum_short$tavg, type ="p", cex =0.1, col ="#00000050", ylab =expression(T[avg]), xlab ="")## draw rectangles with bottom left (100, 300)+i## and top right (150, 380)+irect(0+i, 365+i, -10, 20, col = j, border = j)abline(h = threshold, col ="#660033", lwd =2)
12.2 Gumbellovo rozdělení
Hustota funkce Gumbellova rozdělení je dána předpisem
\[
f(x) = \dfrac{1}{d}\exp\left(-\dfrac{x-c}{d}\right)\cdot\exp\left[-exp\left(-\dfrac{x-c}{d}\right)\right]
\] kde \(c\) a \(d\) jsou parametry. Kvantilová funkce je pak \[
x_T = c - d\cdot\ln\left[-\ln\left(1-\dfrac{1}{T}\right)\right]
\]
kde \(T\) je doba opakování a parametry odhadnuté metodou mometů jsou:
\[
d = \dfrac{\sqrt{6}}{\pi}\sigma, \quad c = \mu-0.5772\cdot d
\]
a \(\mu\)\(\sigma\) jsou momenty celkového souboru.
Kód
fitgumbel <-function(x, ...) { mX <-mean(x) sdX <-sd(x) dX <-sqrt(6)/pi*sdX cX <- mX -0.5772*dXcurve(cX - d*log(-log(1-1/x)), add =TRUE, ...)}plot(x =c(1,100), y =c(0,100), type ="n", xlab ="Doba opakování (roky)", ylab ="Maximální denní průtok v roce (mm/d)")
